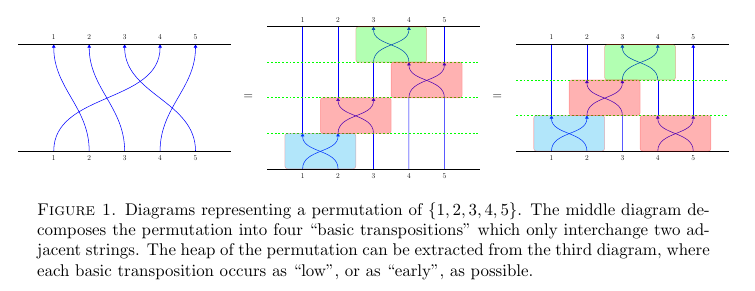
Consider the set S_n of all rearrangments of the numbers 1,2,3,...,n. We may represent each rearrangement in S_n by diagrams like the ones below, where the oriented strings indicate where each number ends up.

Doing so quickly reveals a number of interesting facts about S_n:

• First, we may identify each rearrangment with the function, or permutation, that takes the source of each string to its target. Moreover, composition of these functions can be achieved by stacking the diagrams.
• Second, once we "pull some strings'', we realize that all the diagrams can be obtained by stacking diagrams which only swap two adjacent strings, therefore all the permutations can be obtained by composing those functions which only swap two adjacent numbers.
• Third, we see that some pairs of crossings in a diagram can slide past each other while some cannot. This explains why we are able to push the higher red box in the second picture to the bottom level to get the third picture, but we cannot slide the green box past any red box. It turns out the configuration of the boxes in the third picture, with every boxed pushed as low as possible, forms an interesting object called a heap.

The above story about S_n has an interesting generalization: the set S_n is known as a symmetric group and admits a generalization to Coxeter groups. Coxeter group have rich connections with a field of mathematics called representation theory. Furthermore, we may in fact associate a heap to every so-called fully commutative (FC) element of a Coxeter group. Heaps are closely related to Temperley–Lieb algebras from statistical mechanics and to trace monoids from the theory of concurrent computation in computer science.

The goal of this project is to implement FC elements and their heaps in SageMath, a computer algebra system used by a large number of mathematicians to aid their research. A successful implementation of FC elements and heaps could potentially contribute to current, active research in representation theory.