Abstracts of Invited and Plenary Talks
A PDF version of the schedule, abstracts, and poster titles is
available here.
All talks will be in MacMillan Hall, Room 117. (Enter on
Thayer Street, between Waterman and George).
| Tuesday, August 11 | ||
|---|---|---|
| 9:30–10:00am | Michael Rosen | Opening Remarks |
| 10:00–11:00am | Bjorn Poonen | Heuristics for boundedness of ranks of elliptic curves |
| We present heuristics that suggest that there is a uniform upper bound on the rank of \(E(\mathbb Q)\) as \(E\) varies over all elliptic curves over \(\mathbb Q\). This is joint work with Jennifer Park, John Voight, and Melanie Matchett Wood. | ||
| 11:30–12:15pm | Patrick Ingram | The arithmetic dynamics of correspondences |
| Arithmetic dynamics, like dynamics in general, has largely studied the iteration of functions. It is natural to generalize to the iteration of relations. This talk will survey some recent results in the arithmetic dynamics of correspondences, focusing on questions about the extension to this setting of the Call–Silverman canonical height. | ||
| 2:15–3:00pm | Ian Sprung | The Iwasawa Main Conjecture for elliptic curves at supersingular primes |
| Iwasawa Main Conjectures are equalities between two ideals, one constructed algebraically, the other \(p\)-adic analytically. The elliptic curve Iwasawa Main Conjectures shed some light on the Birch and Swinnerton-Dyer conjectures prime by prime. Ignoring bad reduction primes and some mild assumptions, the status of these main conjectures are as follows: Kato has proved one inclusion ("analytic ideal is inside algebraic ideal") using the method of Euler systems. For the other inclusion, there are two cases. Put \(a_p=p+1-\#E(\mathbb{F}_p)\). When \(p\) is ordinary (i.e. \(p\) and \(a_p\) are coprime), the other inclusion was established by Skinner and Urban using congruences of Eisenstein series. When \(p\) is supersingular (i.e. \(p\) divides \(a_p\)), Wan has proved the other inclusion in the case \(a_p=0\), using congruences of (different) Eisenstein series. In this talk, we present a proof for the general supersingular case. | ||
| 3:00–3:45pm | Rob Benedetto | Determining potential good reduction in arithmetic dynamics |
| Let \(K\) be a non-archimdean field, and let \(\phi(z)\in K(z)\) be a rational function. In 1994, Morton and Silverman defined the notions of good and bad reduction of \(\phi\). It is then natural to define \(\phi\) to have potential good reduction if it is conjugate, possibly over a larger field \(L/K\), to a map of good reduction. In this talk we discuss a simple criterion for determining whether or not \(\phi\) has potentially good reduction. We also consider how large an extension \(L/K\) may be required to exhibit good reduction. | ||
| 4:15–5:15pm | Matt Baker | Lower bounds for average values of Green's functions and applications to canonical heights |
| In their 1988 Inventiones paper, Hindry and Silverman used a Fourier averaging result for certain weighted sums of periodic Bernoulli polynomials in their proof that Szpiro's Conjecture (or equivalently, the \(abc\)-conjecture) implies Lang's conjecture on integral points of elliptic curves and the uniform boundedness of torsion points on elliptic curves over number fields. I will discuss several generalizations of this kind of averaging argument in the context of elliptic curves, metrized graphs, and dynamical systems, along with applications to local and global canonical heights. | ||
| Wednesday, August 12 | ||
| 9:00–10:00am | Jeff Hoffstein | The story of NTRU |
| In 1996 Jill Pipher, Joe Silverman and I came up with a new idea for doing public key cryptography (NTRU). We decided to tell the cryptographic world about it and also to form a company and try to sell it. I will tell you what NTRU was about, and the story of what happened over the next 19 years, during the course of what may have been the slowest get rich quick scheme in history. | ||
| 10:30–11:15am | Katherine Stange | Visualising the arithmetic of imaginary quadratic fields |
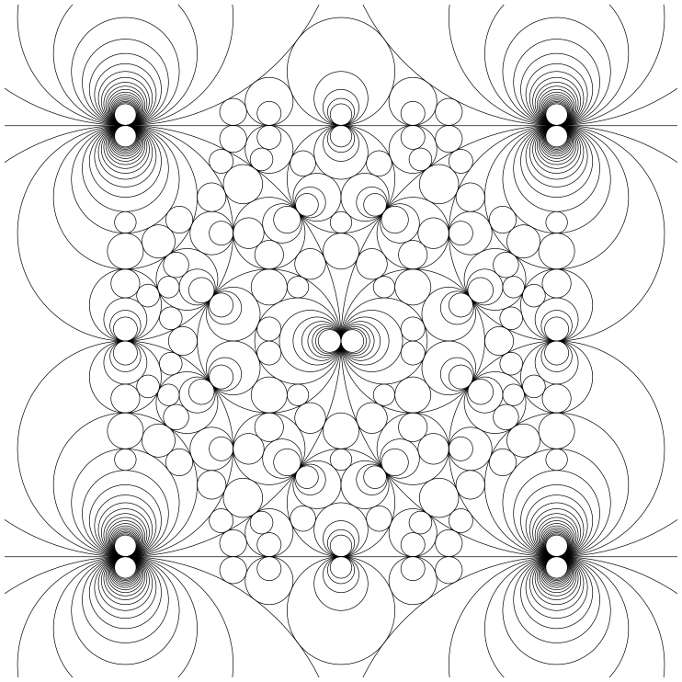
|
Let \(K\) be an imaginary quadratic field with ring of integers \(\mathcal{O}_K\). The Schmidt arrangement of \(K\) is the orbit of the extended real line in the extended complex plane under the Mobius transformation action of the Bianchi group \(\operatorname{PSL}(2,\mathcal{O}_K)\). The arrangement takes the form of a dense collection of intricately nested circles. Aspects of the number theory of \(\mathcal{O}_K\) can be characterised by properties of this picture: for example, the arrangement is connected if and only if \(\mathcal{O}_K\) is Euclidean. I'll explore this structure and its connection to Apollonian circle packings. Specifically, the Schmidt arrangement for the Gaussian integers is a disjoint union of all primitive integral Apollonian circle packings. Generalizing this relationship to all imaginary quadratic \(K\), the geometry naturally defines some new circle packings and thin groups of arithmetic interest. | |
| 11:15–12:15pm | Umberto Zannier | On Silverman's bounded height theorem and unlikely intersections |
| In this talk we shall survey around Silverman's Bounded Height Theorem for sections for families of abelian varieties, especially thinking of certain applications. After recalling a special case, which represents our main purposes, we shall illustrate how this fits within problems of finiteness for "bad specialisations" and Unlikely Intersections in multiplicative tori and abelian varieties, and how useful are Silverman's bounds in the proof of theorems obtained jointly with Amoroso, Bombieri, Corvaja, Masser. | ||
| 2:15–3:00pm | Rachel Pries | Galois action on the homology of Fermat curves |
| Consider the degree \(p\) Fermat curve \(X:x^p+y^p=z^p\) and let \(K={\mathbb Q}(\zeta_p)\). Anderson studied the action of the absolute Galois group \(G_K\) on a relative homology group of \(X\) (Duke, 1987). In particular, he proved that the action factors through the Galois group \(Q\) of the splitting field \(L\) of the polynomial \(1-(1-x^p)^p\) over \(K\). Using this, he obtains results about the field of definition of certain points on a generalized Jacobian of the Fermat curve. We build upon Anderson's work as follows: for an arbitrary prime \(p\) satisfying Vandiver's conjecture, we compute the Galois group \(Q\) and determine an explicit formula for the action of \(q \in Q\) on the relative homology. Using this, we obtain information about maps between several Galois cohomology groups which arise in connection with obstructions to rational points. In particular, this gives information about a differential map arising in the Hochschild-Serre spectral sequence associated with the relevant short exact sequence of Galois groups with restricted ramification. This is joint work with R. Davis, V. Stojanoska, and K. Wickelgren. | ||
| 3:00–3:45pm | Wade Hindes | Prime divisors in dynamical orbits |
| Given a polynomial \(\phi\) over a global field \(K\) and a wandering base point \(b\in K\), we study the set of prime divisors of the orbit \(\mathcal{O}_\phi(b):=\{\phi^n(b)\}_{n\geq0}\). In particular, we use techniques from the theory of rational points on curves and ideas from dynamical Galois theory to compute the density of such sets of primes. | ||
| 3:45–5:30pm | Tea & Poster Session | |
| Thursday, August 13 | ||
| 9:00–10:00am | Laura DeMarco | Variation of canonical height, illustrated |
| Around 1990, Joe Silverman wrote a series of three articles on the variation of canonical height in families of elliptic curves. I will discuss connections between these results and dynamical systems on \(\mathbb{P}^1\). As the height functions define dynamical "bifurcation measures" on the base variety, I will show illustrations of these measure densities in some examples. | ||
| 10:30–11:15am | Masato Kuwata | Elliptic K3 surfaces with Mordell-Weil rank 18 |
| The rank of the Mordell-Weil group of an elliptic K3 surface over a field of characteristic 0 can be as high as 18. Examples of such elliptic K3 surfaces can be constructed from isogenous pairs of elliptic curves with complex multiplication. More precisely, they are constructed as finite coverings of the Kummer surface associated with the product of such pairs of elliptic curves. The determination of the rank of the Mordell-Weil group for such elliptic surfaces depends on a theorem of Inose, which relies on a transcendental argument, and we have not had a good understanding of the structure of the Mordell-Weil group itself. In this talk we describe the field of definition of the Mordell-Weil groups of such elliptic surfaces and give an explicit description of their generators. This is joint work with Abhinav Kumar. | ||
| 11:15–12:15pm | Marc Hindry | Brauer-Siegel ratio for abelian varieties over global fields |
| This is a partial attempt to answer the question of how large must be the size of generators of the Mordell-Weil group. To study this we consider a family of ablian varieties of fixed dimension over a global field (a number field or the function field of a curve over a finite field). Assume finiteness of the Shafarevic-Tate group. We study the asymptotic behaviour of the product of the cardinality of the Shafarevic-Tate group by the Néron-Tate regulator, comparing it with the exponential height. Some examples of families show asymptotics similar to the classical Brauer-Siegel theorem, but others suggest a different behaviour. Results over number fields are, alas, all conditional, but the situation is better over function fields. We also prove in this context interesting inequalities linking heights, conductors and the number of components of the Néron model. A large part of this work is a collaboration with Amílcar Pacheco. | ||
| 2:15–3:15pm | Lucien Szpiro | Self-maps of \(\mathbb{P}^1\) with fixed degeneracies |
| We introduce a new notion: critically excellent reduction for a self-map of \(\mathbb{P}^1_K\), where \(K\) is a number field or a function field. This allows us to prove a finiteness theorem for the set of conjugacy classes of tame self-maps of \(\mathbb{P}^1_K\) of a given degree \(d\ge2\) having critically excellent reduction outside of a given finite set \(S\) of places of \(K\). It is the solution to the "Shafarevich problem" for self-maps of \(\mathbb{P}^1_K\). (joint work with Tom Tucker and Lloyd West) | ||
| 3:45–4:30pm | Arthur Baragar | Interpreting Euclidean structure in the ample cone for elliptic K3 surfaces |
| Let \(X\) be a K3 surface fibered by elliptic curves together with a section. In this talk, we connect certain Euclidean-geometric structure in the ample cone for \(X\) with the group structure of the elliptic curves in the fibration, and the Neron-Tate pairing on those curves. This is related to the specialization theorem. | ||
| 4:30–5:15pm | Holly Krieger | A case of the dynamical André-Oort conjecture |
| I will discuss the dynamical André-Oort conjecture proposed by Baker-DeMarco, focusing on a case suggested by Ingram and recently proved by Ghioca, Nguyen, Ye, and myself: if \(C\) is an irreducible plane curve containing infinitely many points \((a,b)\) for which \(z^d+a\) and \(z^d+b\) are both post-critically finite, then \(C\) is a fiber of a projection, or the zero locus of \(h(x) = Ax\) for some \((d-1)\)st root of unity \(A\). The proof includes an analysis of the existence of linear maps on angles of external rays of the Mandelbrot set. | ||
| Friday, August 14 | ||
| 9:00–10:00am | David Masser | Specializations and bounded height |
| After the work of Silverman and Manin-Demjanenko it was natural to ask if the absolute heights of numbers \(\alpha\) defined by multiplicative equations such as \(\alpha^r(1-\alpha)^s=1\) are bounded above independently of the integers \(r,s\) (here not both 0). In the more general context of algebraic curves in \(\mathbf{G}_{\text{m}}^n\) this was answered affirmatively in 1999. Here we present a generalization, obtained with Amoroso and Zannier, of which the corresponding assertion for \(\alpha^r+(1-\alpha)^s=1\) is a very special case (now with \(r,s\) not both 1). | ||
| 10:30–11:15am | Bianca Viray | Obstructions to the Hasse principle on Enriques surface |
| In 1970, Manin showed that the Brauer group can obstruct the existence of global rational points, even when there exist points everywhere locally. Later, Skorobogatov defined a refinement of this Brauer–Manin obstruction, called the étale-Brauer obstruction. We show that this refined obstruction is necessary to understand failures of the Hasse principle on Enriques surfaces, thereby completing the case of Kodaira dimension 0 surfaces. This is joint work with F. Balestrieri, J. Berg, M. Manes, and J. Park. | ||
| 11:15–12:15pm | Shu Kawaguchi | Around canonical heights in arithmetic dynamics |
| In the early 90s, in the papers "Rational points on K3 surfaces: a new canonical height" and "Canonical heights on varieties with morphisms," Silverman and Call–Silverman constructed canonical heights, which are similar to Néron–Tate heights on abelian varieties, and they studied arithmetic and dynamical properties of varieties with morphisms. Over the recent years, there have been a flourish of diverse studies on arithmetic and dynamical properties of varieties with morphisms (and rational maps). In this talk, which is mostly a survey, we would like to see some developments around canonical heights and height growth rates in arithmetic dynamics. | ||
| 2:15–3:15pm | Paul Vojta | Recent applications of Schmidt's subspace theorem |
| In 2002, Corvaja and Zannier obtained a new proof of Siegel's theorem (on integral points on curves) based on Schmidt's celebrated Subspace Theorem. Soon after that (and based on earlier work), Evertse and Ferretti applied Schmidt's theorem to give diophantine results for homogeneous polynomials of higher degree on a projective variety in \(\mathbb P^n\). This has led to further work of A. Levin, P. Autissier, M. Ru, G. Heier, and others. In particular, Ru has defined a number, \(\operatorname{Neva}(D)\), that concisely describes the best diophantine approximation for an effective divisor \(D\) on a projective variety \(X\). In this talk, I will give an overview of this area of research, and indicate how an example of Faltings can be described using \(\operatorname{Neva}(D)\). | ||
| Saturday, August 15 | ||
| 9:00–10:00am | Felipe Voloch | Waring’s problem for polynomials |
| We will discuss Waring’s problem for polynomials, from two viewpoints. First from a geometric approach using surfaces in positive characteristics and then from a more algebraic approach, using roots of unity. | ||
| 10:30–11:15am | Rafe Jones | An arithmetic dynamical Mordell-Lang conjecture |
| The dynamical Mordell-Lang conjecture asserts that an orbit of an endomorphism of a variety (over \(\mathbb C\)) can intersect a subvariety only in a rigid way: the index set of the intersection must be a finite union of arithmetic progressions. In this talk I ask whether an arithmetic version of this conjecture might hold: if the variety and morphism are defined over a number field \(K\), must a \(K\)-orbit intersect the value set of any other \(K\)-endomorphism in a similar rigid way? I will give heuristics suggesting the answer may well be yes, and describe recent results showing the answer is in fact yes when the variety is the projective line and the value set is that of the \(m\)'th power map \((m \gt 1)\). A corollary is that if a \(K\)-orbit of a rational function has infinite intersection with the set \(K^m\) of \(m\)'th powers (\(m \gt 2\)), then the orbit cannot have more than \(m-1\) consecutive terms that fail to be \(m\)'th powers. For \(m = 2\), exceptions arise in the form of certain Lattes maps attached to elliptic curves with complex multiplication. | ||
| 11:15–12:15pm | Michael Rosen | An elementary proof of the Kronecker–Weber theorem in function fields |
| This talk will present an elementary proof of the the function field version of the Kronecker-Weber theorem over the rational function field. The proof uses facts from the Lubin–Tate theory of formal groups. A sketch will be given of the general case (arbitrary global function field as base) using an extension of Lubin–Tate theory due to E. de Shalit. | ||
Return to the conference schedule.